13. Dynamiske systemer

Krefter og bevegelse

Oppgave 1

a) Tegningen bør inneholde en kraftpil for gravitasjonen, og en for luftmotstand.

b) Når vi ser bort fra luftmotstanden har vi fra Newtons 2. lov at:

$$\sum F=ma$$

$$\sum F=-G=-mg$$

$$ma=-mg$$

$$a=-g$$

Siden akselerasjonen er konstant lik -9.81 (forutsatt havnivå og positiv retning valgt oppover), kan vi finne v og s ved å bruke bevegelseslikningene for konstant akselerasjon.

c)

Vi kan lage en modell med kvadratisk luftmotstand. Deretter kan du i d) eksperimentere med en lineær luftmotstand og ulike verdier av k. I uttrykket for luftmotstand bruker vi $L=-k\cdot |v|\cdot v$ for at luftmotstanden skal være motsatt rettet av hastigheten.

import numpy as np
import matplotlib.pyplot as plt

# Konstanter
m = 5.0E-7       # masse i kg
g = 9.81         # tyngdeakselerasjon i m/s^2
k = 1.9E-7       # luftmotstandskoeffisien for vanndråpen
v0 = 0           # startfart
s0 = 0           # startposisjon i y-retning

# Tidsparametere
dt = 0.01        # tidsintervall
T = 5            # sluttiden
N = int(T/dt)+1  # antall iterasjoner

# Arrayer
t = np.zeros(N)
v = np.zeros(N)
s = np.zeros(N)

# Initialiserer arrayene
s[0] = s0
v[0] = v0

for i in range(N-1):
    a = -g - k*v[i]*abs(v[i])/m
    v[i+1] = v[i] + a*dt
    s[i+1] = s[i] + v[i]*dt
    t[i+1] = t[i] + dt
    
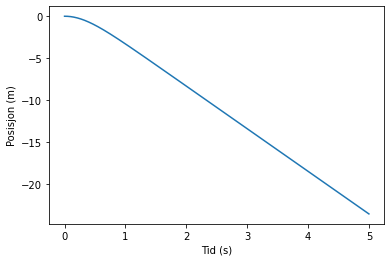
plt.plot(t,s)
plt.xlabel('Tid (s)')
plt.ylabel('Posisjon (m)')
plt.show()

Populasjonsdynamikk

Oppgave 2

a) Faktorer som påvirker slike populasjoner er blant annet plass, årstidsvekslinger, tilgang til mat og vann, stress, sykdom og parasitter. Vi trenger ikke nødvendigvis å ta hensyn til bæreevnen til ugla, fordi modellen tar utgangspunkt i at ugla begrenses av musepopulasjonen.

b) Vi kan bruke Lotka-Volterra-likningene til å modellere populasjonsveksten.

$$M^{\prime }(t)=aM(t)(1-\frac{M(t)}{b})-cM(t)U(t)$$

Her er $M^{\prime }(t)$ endringen i antall mus, justert av vekstraten $a$. Denne er avhengig av faktorene som er nevnt i a). Konstanten $b$ er bæreevnen som begrenser antall individer i populasjonen, og $c$ er både naturlig dødsrate og møteraten mellom ugler og mus. Denne konstanten er spesielt avhengig av tettheten til populasjonene, og hvilket miljø de lever i. For å beskrive endringen i uglepopulasjonen, $U^{\prime }t()$ kan vi bruke følgende sammenheng:

$$U^{\prime }(t)=dM(t)U(t)-eU(t)$$

Her er $d$ en kombinert fødsels- og møterate for uglene. Konstanten $d$ vil ofte være lavere enn $c$ fordi et møte mellom ugle og mus ofte resulterer i at en mus dør, men ikke at en ny ugle blir født! Konstanten $e$ er naturlig dødsrate.

c) En programskisse kan se slik ut:

Konstanter: a,b,c,d,e,M0,U0
Tidsvariabler: dt, tid_slutt, N
Arrayer: M, U, t
Startverdier av arrayer

Gjenta N-1 ganger:
    Mder = aM(1-M/b) - cMU
    Uder = dMU - eU
    M = M + Mder*dt
    U = U + UDer*dt
    t = t + dt

d) Vi kan kopiere plottemetoden fra boka, men det er lurt å lage resten selv. Vi velger tid, konstanter og tid som vi ønsker. Deretter kan vi gjerne evaluere resultatene og gjøre nye valg basert på dette.

import matplotlib.pyplot as plt
import numpy as np

#Initialbetingelser
M0 = 100          # antall mus ved t = 0
U0 = 5            # antall ugler ved t = 0
a = 0.11          # reproduksjonsrate, mus
b = 10000         # bæreevne, mus
c = 0.004         # mus-ugle møterate
d = 0.000034      # reproduksjon og mat, ugler
e = 0.055         # dødsrate for ugler

#Tidssteg
dt = 0.001        # tidssteg
tid = 200         # antall uker
N = int(tid/dt)+1 # antall intervaller

#Arrayer
t = np.zeros(N)
M = np.zeros(N)
U = np.zeros(N)

# Initierer arrayene
M[0] = M0
U[0] = U0

# Eulers metode
for i in range(N-1):
    Mder = a*M[i]*(1 - M[i]/b)  - c*M[i]*U[i]
    Uder = d*M[i]*U[i] - e*U[i]
    M[i+1] = M[i] + Mder*dt
    U[i+1] = U[i] + Uder*dt
    t[i+1] = t[i] + dt

# Plotting
fig = plt.figure()
ax = fig.add_subplot(111)
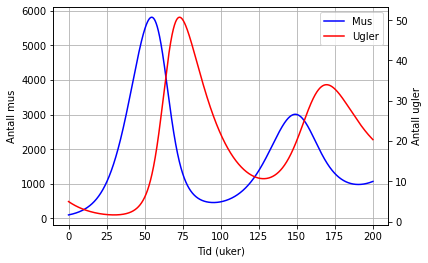
data1 = ax.plot(t, M, '-b', label = 'Mus')
ax2 = ax.twinx()
data2 = ax2.plot(t, U, '-r', label = 'Ugler')

data = data1 + data2
datatittel = [l.get_label() for l in data]
ax.legend(data, datatittel, loc=0)

ax.grid()
ax.set_xlabel("Tid (uker)")
ax.set_ylabel("Antall mus")
ax2.set_ylabel("Antall ugler")
plt.show()

Reaksjonsfart

Oppgave 3

import numpy as np
import matplotlib.pyplot as plt

# Konstanter
k0 = 0.003627
kH = 7106.41
H = 1.26E-7

# Tidsparametere
t0 = 0
tid_slutt = 600 # Tid i minutter
dt = 1E-3
N = int((tid_slutt-t0)/dt) + 1

# Arrayer
A = np.zeros(N)
S = np.zeros(N)
t = np.zeros(N)

# Ratelovene
def dA(A):
    return -(k0 + kH*H)*A

def dS(A):
      return (k0 + kH*H)*A

# Forward Euler
def euler(A0, S0):
    A[0] = A0
    S[0] = S0
    for i in range(N-1):
        A[i+1] = A[i] + dA(A[i])*dt
        S[i+1] = S[i] + dS(A[i])*dt
        t[i+1] = t[i] + dt
    return A, S, t

A, S, t = euler(1, 0)

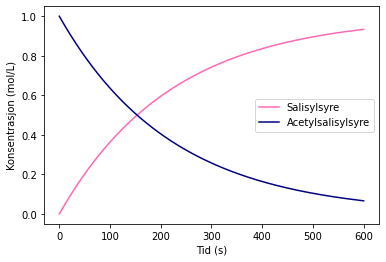
plt.plot(t,S, label = 'Salisylsyre', color = 'hotpink')
plt.plot(t,A, label = 'Acetylsalisylsyre', color = 'navy')
plt.xlabel('Tid (s)')
plt.ylabel('Konsentrasjon (mol/L)')
plt.legend(loc=0)
plt.show()